Scribe # (insert actual number here)

Yo. This is Van, doing the scribe, and if I didn't have enough work to do already, Calvin felt like messing me up with the scribe for today (sorry if that's inappropriate, I'll change it later if need be, but if it's funny, then I've succeeded in my goal that tried to be slighty humorous). ANYWAYS, onto the scribe which has, 3 pictures. Teddie's right, pictures are actually fun to make... till Paint gets annoying.

So today, we have a double class, (even more reason for me to spite Calvin) and we learn what the focus and directrix means. Meanwhile, Mr.K goes off topic, and onto the USE of these parabolas. He also spites MTS, because he says "What does the rain have to do with my Cable/internet?". So he draws a picture of how we get the signal onto our tv and watch it!

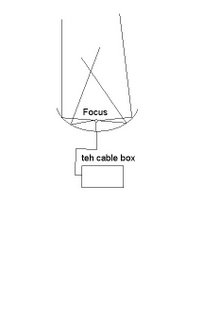
So, the focus, is recieving concentrated signals from the distributors, and the cable box has to be activated to descramble the signal. "Neat stuff he says". "You should go into computer science.". "Wanna make a LOT of money?, Go into MATH". Then he talks about how Amazon.com is cool and how mathamatizing humanity is in progress. Of course, everyone is dumbfounded. I'm off topic myself, off to the real stuff we're supposed to learn. So after his ranting about the parabola and satelites, we begin to write in our math dictionaries!. (Oh joy)










Parabola - The Locus of points that are equidistant from a Fixed line (directrix) and a Fixed point (focus).

The Anatomy of a Parabola

Equation
(x-h)² = 4p(y- k)

Properties
P>0 opens up
P<0 style="color: rgb(51, 51, 255);">Focus at (h, k+p)
Equation of Directrix y= k - p
Equation of axis of symmetry x=h
If |4p| > 1 arms are "wide"
If |4p| <>







Equation
(y-k)² = 4p(x-h)

Properties
P>0 opens right
P<0 style="color: rgb(0, 0, 0);">Vertex at (h,k)
Focus at (h+p, k)
Equation Of Directrix y= h-p
Equation of axis of symmetry y=k
If |4p| > 1 arms are "wide"
If |4p| <>Deriving the Standard Form for the Equation of a Vertical Parabola



















__ __
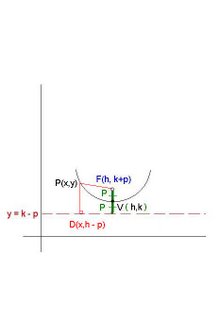
PD = PF [By Definition]

(y- x)²+[y-(k-p)]² = (x-h)²+(y-[x+p])² [Distance Formula]
(y- k+p)² = (x-h)² + (y- k- p)² [Square both sides & simplify] *Desregard red line on "2kp"
y² - 2ky + 2py - 2kp + k² + p² = (x-h)² + y² - 2ky+ 2kp + k² + p² [expanding]
2py - 2pk = (x-h)² + 2kp + 2py [Balancing]
4py - 4pk = (x-h)² [Balancing]
4p(y-k) = (x-h)² [Factor out 4p]



Okay I'm done the scribe!, Huzzah!. Woohoo, one hour and a half hours invested and time to work on english. Sorry for the late scribe. The next scribe will be Abdi. Enjoy people.

i'm gonna edit this later, someone tell me how to place a square root over a long line of things, and i'll change it