Scribe #22

Hey guyzzz.... It's me again, Emile your scribe for Friday, March 10,'06. The first part of the class in the morning, we had a debate about what time would be the test? The majority decided that we held the test in the afternoon.

After the class debate, Mr. K asked us, if we have any question involving any topic in transformation and word problems. Some of our classmates asked about the even and odd functions. Here are some examples:

An example of even function:

f(-x)= f(x)

f(x)= 2x²-4

f(-x)= 2(-x)²-4
f(-x)= 2x²-4; It is an even function because f(-x)=f(x).


An example of an odd function:

f(-x)= -f(x)

f(-x)= (-x)³-(-x)
f(-x)= -x³+x

-f(x)= -(x³-x)
-f(x)= -x³+x; In this case it is an odd function because f(-x)= -f(x).


Another issue was brought in and it was the reciprocal function or 1/f(x). And it was like this:

f(x)= 2x²-4

Then half part of morning of the class we wrote something in our Math Dictionary about:


The other Trig Functions

The Tangent Function

f(x)= tanx
















Properties of the Tangent functions

Domain:{xlx is not equal pi/2+kpi; k is an element of I, x is and element of R}
Range: (-00,00) or {yly is an element of R}
Amplitude: undefined
Period: pi
Roots: kpi ; k is an element of I



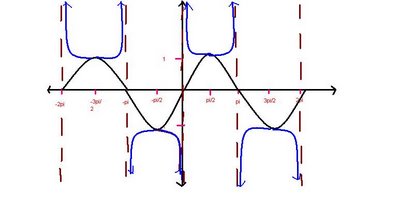
The Cosecant Function

f(x)=cscx= 1/sinx

Properties of the cosecant function:

Domain: { xlx not equal k pi; kis an elemnt of I, x is an element of R}
Range: (-00,-1] U [1,00)
Amplitude:undefined
Period: 2pi
Roots: none
y-intercept: none
Symmetry: an odd function


That's all for me now. Oops! before I forget the next scribe is Teddie. A tout à l'heure.